Как атом решает какой фотон поглотить. Физики впервые увидели столкновение фотона с фотоном. Суммарное сечение взаимодействия фотонов с веществом

11 июня 2020

Кривая поглощения

К γ-излучению относят электромагнитные волны, длина волны которых значительно меньше межатомных расстояний, т.е. λ < а, где а ~ 10 -8 см. Таким образом, нижний предел энергии γ-квантов получается Е = hν = hc/λ. = 12 кэВ.
Подобно заряженным частицам, поток фотонов поглощается веществом в основном за счет электромагнитного взаимодействия. Однако механизм этого поглощения существенно иной. На это есть две причины:
1) фотоны не имеют электрического заряда и, следовательно, не подвержены влиянию дальнодействующих кулоновских сил. Поэтому при прохождении через вещество фотоны сравнительно редко сталкиваются с электронами и ядрами, но зато при столкновении, как правило, резко отклоняются от своего пути, т.е. практически выбывают из пучка;
2) фотоны обладают нулевой массой покоя и, следовательно, не могут иметь скорости, отличной от скорости света. А это значит, что в среде они не могут замедляться. Они либо поглощаются, либо рассеиваются, причем в основном на большие углы. При прохождении пучка фотонов через вещество в результате взаимодействий со средой постепенно ослабляется интенсивность этого пучка. Найдем закон, по которому происходит это ослабление, т.е. кривую поглощения фотонов в веществе.

Пусть на поверхность плоской мишени перпендикулярно ей падает поток фотонов J 0 см -2 с -1 (рис. 3.1), и толщина мишени х (см) настолько мала, что происходит лишь однократное взаимодействие. Изменение интенсивности этого потока dJ при прохождении фотонами слоя вещества dx пропорционально величине потока J на глубине этого слоя, толщине слоя dx (см), плотности атомов n(см -3) и эффективному сечению взаимодействия фотонов σ (см 2):

Решение этого уравнения дает кривую поглощения

J x = J 0 e -σnx .

Обычно с поглощением фотонов в веществе связывают два понятия.

Линейный коэффициент поглощения τ = nσ; [τ] = см -1 и J x = J0e -τx . Таким образом τ − эта такая толщина вещества в сантиметрах, на которой поток фотонов ослабляется в е раз.
Массовый коэффициент поглощения μ = τ/ρ = σn/ρ, где ρ (г/ см) − плотность вещества. Размерность μ получается следующей: [μ] = см 2 /г. При этом изменение потока фотонов принимает вид:

J x = J 0 е -μxρ ,

где хρ (г/см 2) − толщина вещества, измеренная в массовых единицах. Смысл тот же − эта такая толщина вещества в г/см 2 , на которой поток ослабляется в е раз.

Коэффициент поглощения полностью характеризует прохождение фотонов через вещество. Он зависит от свойств среды и энергии фотонов. Если поглощение идет за счет нескольких различных процессов, каждому из которых соответствует свой коэффициент поглощения, μ i , τ i ,…, то полный коэффициент поглощения μ = ∑μ i и τ = ∑τ i
Поглощение фотонов веществом в основном происходит за счет трех процессов: фотоэффекта, комптон-эффекта и рождения электронно-позитронных пар в кулоновском поле ядра.

3.2 Фотоэффект

Фотоэлектрический эффект − это освобождение электронов, находящихся в веществе в связанном состоянии, под воздействием фотонов. Различают внутренний фотоэффект и внешний.
Внутренним фотоэффектом называют переходы электронов под воздействием электромагнитного излучения внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу.
Внешний фотоэффект наблюдается в твердых телах, газах, на отдельных атомах и молекулах — это испускание электронов наружу при поглощении фотонов. В этих лекциях будет обсуждаться только внешний фотоэффект. Фотоэффектом будем называть процесс, при котором атом поглощает фотон и испускает электрон. При этом падающий фотон взаимодействует со связанным в атоме электроном и передает ему свою энергию. Электрон получает кинетическую энергию Т е и покидает атом, а атом остается в возбужденном состоянии. Поэтому фотоэффект всегда сопровождается характеристическим рентгеновским излучением атома или испусканием электронов Оже. При эффекте Оже происходит непосредственная передача энергии возбуждения атома одному из его электронов, который в результате этого покидает атом. Законы сохранения энергии и импульса при фотоэффекте могут быть представлены в виде:

hν = Т е + I i + Т я, и

где , − кинетическая энергия ядра отдачи; I i − энергия ионизации
i-й оболочки атома; . Так как обычно hν >> I i + Т я, то энергия фотоэлектронов Т е ≈ hν, и, следовательно, энергетический спектр фотоэлектронов близок к монохроматическому.
Из законов сохранения энергии и импульса следует, что фотоэффект не может происходить на свободном электроне. Докажем это «от противного»: предположим, что такой процесс возможен. Тогда законы сохранения будут выглядеть так

Отсюда получаем уравнение 1 − β = √1 − β 2 , которое имеет два корня β = 0 и β = 1. Первый из них соответствует Т е = hν = 0, а второй не имеет физического смысла для частиц с массой отличной от нуля.
Еще нагляднее это доказательство выглядит для нерелятивистского случая: hν = m e v 2 /2 и hν/c = m e v. Решение системы приводит к выражению v = 2с, чего не может быть.
Таким образом, свободный электрон не может поглощать фотон. Для фотоэффекта существенна связь электрона с атомом, которому передается часть импульса фотона. Фотоэффект возможен лишь на связанном электроне. Чем меньше энергия связи электрона с атомом по сравнению с энергией фотона, тем менее вероятен фотоэффект. Это обстоятельство определяет все основные свойства фотоэффекта:

A) ход сечения с энергией фотона − σ ф (hν) , b) соотношение вероятностей фотоэффекта на разных электронных оболочках, c) зависимость сечения от Z среды.

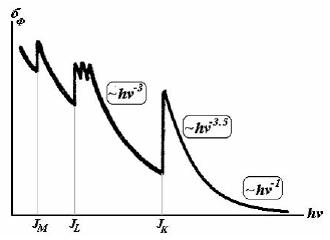Рис.3.2. Зависимость эффективного сечения фотоэффекта от энергии фотонов

a) На рис.3.2 изображена зависимость эффективного сечения фотоэффекта от энергией фотонов. Если энергия фотона велика по сравнению с энергией связи электронов в атоме, то сечение фотоэффекта оф быстро убывает с увеличением энергии фотона. При I i << hν < m e c 2 σ ф ~ (hν) -3.5 .
При hν > m e c 2 σ ф ~ (hν) -1 .
По мере убывания hν, т.е. возрастания связности электронов I k /hν, сечение процесса быстро растет до тех пор, пока энергия фотона не станет равной энергии I k . При hν < I k фотоэффект на K-оболочке атома станет невозможным, сечение фотоэффекта будет определяться только взаимодействием фотонов с электронами L, М и др. оболочек. Но эти электроны связаны с ядром слабее, чем
K-электроны. Поэтому при равных энергиях фотонов вероятность фотоэффекта на L-электронах много меньше, чем на K-электронах. В зависимости σ ф (hν) будет наблюдаться резкий скачок. Затем при
hν < I k снова σ ф начинает расти с убыванием hν, так как возрастает относительная связность электрона L/hν, и т.д.
b) Формулы для сечения фотоэффекта на K-электронах, полученные методами квантовой электродинамики и подтвержденные экспериментом, имеют вид:

Отношения сечений фотоэффекта на разных оболочках получаются следующими:

Поэтому при вычислении полного сечения фотоэффекта обычно используется соотношение:

с) Из этой же формулы видна сильная зависимость σ ф от Z среды: σ ф ~ Z . Это понятно, так как в легких элементах электроны связаны кулоновскими силами ядра слабее, чем в тяжелых. В тяжелых веществах фотоэффект является главной причиной поглощения мягких фотонов.
Угловое распределение фотоэлектронов получается расчетным путем из формулы для дифференциального сечения. Из нее следует, что фотоэлектроны распределены симметрично по закону ~ cos 2 φ относительно направления электрического вектора падающей электромагнитной волны. Кроме того, угловое распределение существенно зависит от энергии фотоэлектронов. В нерелятивистском случае Т е << m е c 2 (β << 1) интенсивность фотоэлектронов максимальна в плоскости поляризации векторов и фотона, т.е. в плоскости, перпендикулярной направлению движения фотона. При больших энергиях Т е > m е c 2 угол, под которым интенсивность фотоэлектронов максимальна, уменьшается, причем чем больше энергия электронов, тем меньше угол их вылета по сравнению с направлением движения фотона, угловое распределение получается вытянутым вперед.

3.3. Комптон-эффект

Взаимодействие фотонов с веществом может приводить к их рассеянию без поглощения. Рассеяние может быть двух видов: 1) без изменения длины волны (когерентное рассеяние, томсоновское, классическое) и 2) с изменением длины волны (некогерентное, комптоновокое рассеяние).

1. Томсоновское рассеяние происходит, если hν < I i (λ ~10 -8 см). В этом случае атом воспринимается фотоном «как единое целое», и фотон обменивается энергией и импульсом со всем атомом. Так как масса атома очень велика по сравнению с эквивалентной массой фотона hν/c , то отдача в этом случае практически отсутствует. Поэтому рассеяние фотонов происходит без изменения их энергии, т.е. когерентно.
Можно считать, что источником рассеянного излучения являются связанные электроны атома, которые приходят в резонансные колебания под действием падающего излучения и, вследствие этого, излучают фотоны такой же частоты. Сечение томсоновского рассеяния зависит от угла рассеяния фотона 0:

σ(θ) = 0.5r e 2 (l + cos 2 θ),

где r e 2 = е 2 /m е c 2 = 2.8·10 -13 см − классический радиус электрона. Интегрируя по всем θ можно получить сечение полного томсоновского рассеяния. Эффективное сечение томсоновского рассеяния, рассчитанное на 1 электрон, равно:

σ T = (8/3)πr e 2 = 0.66 барн,

где σ T − универсальная постоянная и не зависит от частоты падающего излучения.

2. Комптоновское рассеяние возникает при hν >> I i . В этом случае все электроны атома можно считать свободными.

Комптоновское рассеяние происходит в результате упругого столкновения фотона с электроном, причем фотон передает электрону часть своей энергии и импульса. Поэтому энергетические и угловые характеристики явления полностью определяются законами сохранения энергии и импульса для упругого удара (рис. 3.3):

hν = hν« + Т е,

где и − кинетическая энергия и импульс электрона отдачи.

Совместное решение этих уравнений позволяет получить энергии рассеянного фотона hν« и электрона отдачи Т е в зависимости от угла рассеяния фотона θ:

Из этих соотношений вытекает ряд важных следствий.

1. Из первого соотношения легко найти, на сколько изменилась длина электромагнитной волны при комптоновском рассеянии (формула Комптона):

где λ 0 = h/m e c = 2.426·10 -10 см − комптоновская длина волны электрона. Из формулы Комптона следует, что:

A) сдвиг волны Δλ не зависит от величины длины волны; b) сдвиг Δλ, определяется лишь углом рассеяния фотонов θ: при θ = 0 Δλ = 0 (т.е. нет рассеяния), при θ = π/2 Δλ = λ 0 и при θ = π, Δλ = 2λ 0 (максимально возможный сдвиг происходит при рассеянии назад).

2. Энергетический спектр фотонов, полученный в результате комптоновского рассеяния пучка моноэнергетических γ-квантов, оказывается непрерывным в интервале энергий от

при θ = πдо hν max = hν при θ = 0.

3. В результате комптоновского рассеяния моноэнергетических γ-квантов получается непрерывный энергетический спектр электронов отдачи в интервале от

T e min = 0 при θ = 0 до при θ = π.

4. Связь углов вылета рассеянного фотона θ и электрона отдачи φ (рис.3.3) можно найти из закона сохранения импульса, записанного для продольной и поперечной составляющих (относительно направления движения первичного фотона):

Преобразуем второе уравнение:

Отсюда находим:

Из полученного соотношения видно, что изменению угла рассеяния фотона в интервале 0 ≤ θ ≤ π соответствует изменение угла вылета электрона отдачи в интервале π/2 ≥ φ ≥ 0. Таким образом, электроны вылетают только в переднюю полусферу, причем наиболее энергичные электроны летят в направлении первичного фотона.
Дифференциальное эффективное сечение комптоновского рассеяния было впервые рассчитано О. Клейном и И . Нишиной в 1929 г., а в 1930 г. эту же формулу другим способом получил И.Е.Тамм. Формула Клейна-Нишины-Тамма имеет вид:

где dσ K /dΩ − дифференциальное эффективное сечение рассеяния фотона под углом θ в телесный угол dΩ, а r е − классический радиус электрона. После подстановки в эту формулу значения hν« получается зависимость дифференциального сечения комптоновского рассеяния только от hν и от θ, причем форма зависимости сечения от θ меняется с изменением энергии фотонов. При малых значениях hν:
dσ K /dΩ ~ 1 + cos 2 θ. С ростом hν все большее количество фотонов рассеивается в направлении «вперед», причем с увеличением первичной энергии hν повышается вероятность рассеяния на малые углы (рис.3.4).
Полное сечение находится после интегрирования по всем θ:

где σ T = (8π/3)r e 2 − сечение томсоновского рассеяния, а ƒ(hν/m e c 2) < 1 и возрастает с увеличением hν.
При малых значениях hν (I K << hν/m e c 2 <<1), σ K ~ σ T ·(1 − 2hν/m e c 2) → σ T с уменьшением hν.

Так как в 1см среды находится Zn электронов, то полная вероятность комптоновского рассеяния на 1см пути в веществе (Z,A,ρ) будет:

Таким образом, вероятность комптоновского рассеяния на 1 см пути обратно пропорциональна энергии фотонов и пропорциональна Z вещества (сечение в расчете на 1 электрон не зависит от Z вещества, а каждый атом содержит Z электронов). На рис.3.5 изображен график зависимости σ K /σ T от энергии фотонов. На этом рисунке приведены в тех же единицах сечение фотоэффекта в различных веществах. Сравнение зависимостей показывает, что с повышением энергии фотонов вероятность комптон-эффекта становится существенно больше сечений фотоэффекта.

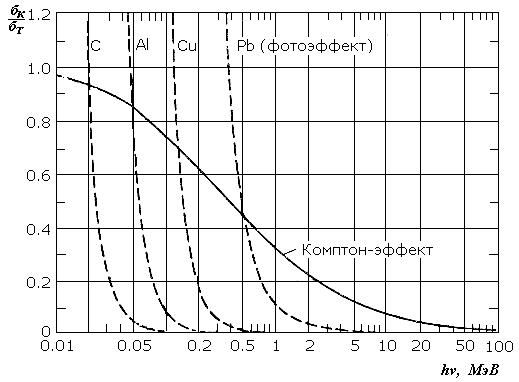
Рис.3.5. Зависимость полных сечений комптоновоского рассеяния (сплошная кривая) и фотоэффекта в пересчете на 1 электрон (пунктир для С, А1, Си и Рb) от энергии фотонов

Комптоновское рассеяние может происходить не только на электронах, но и на других частицах, имеющих электрический заряд. Однако вероятность такого эффекта очень мала. Например, комптоновское рассеяние на ядрах атомов пренебрежимо мало из-за того, что у ядер очень мала величина их классического электромагнитного радиуса Ze 2 /m я с 2 .
Существует еще явление, называемое обратным комптон-эффектом. Оно происходит при упругом рассеянии фотонов на релятивистских электронах. В этом случае энергия и импульс фотонов будут увеличиваться за счет энергии и импульса электронов-мишеней.

3.4. Рождение электронно-позитронных пар

При достаточно большой энергии фотонов (hν > 2m e c 2) становится возможным процесс образования пары, при котором в поле ядра фотон поглощается, и рождаются электрон и позитрон. Расчет по КЭД и опыт свидетельствуют о том, что этот процесс происходит не внутри ядра, а около него, в области, имеющей размер комптоновской длины волны λ 0 = 2.4·10 -10 см. Поскольку при этом взаимодействии фотона с полем ядра рождаются электрон и позитрон, то этот процесс имеет энергетический порог, т.е. он происходит, если hν > 2m e c 2 . Законы сохранения энергии и импульса могут быть записаны в виде:

hν = 2m e c 2 + Т − + Т + + Т я,

где β − и β + − относительные скорости электрона и позитрона, Т − и Т + − их кинетические энергии, а Т я и р я − энергия и импульс ядра отдачи.
Исходя из законов сохранения энергии и импульса, можно показать, что образование электронно-позитронной пары фотоном в вакууме невозможно: энергия и импульс обязательно должны распределяться между тремя частицами: электроном, позитроном и, например, ядром. Если предположим, что рождение пары может происходить в вакууме (Т я = р я = 0), то законы сохранения принимают вид:

hν = 2m e c 2 + Т − + Т + и

Первое из этих уравнений можно записать в форме:

и сразу же становится очевидной его несовместимость со вторым уравнением.
В частном случае, когда Т − = Т + = 0, получается система противоречивых уравнений: hν = 2m e c 2 и
hν/c = 0. Таким образом, чтобы выполнялись законы сохранения, нужна третья частица, в поле которой происходит процесс рождения пары и которая принимает на себя избыточный импульс. Такой частицей может быть не только ядро, но и, например, электрон. Но если у ядра Т я = р я 2 /2m я − малая величина, то у электрона отдача будет очень большая, и электрон отдачи может получить энергию того же порядка, что и компоненты пары. В этом случае порог процесса будет существенно превышать 2m e c 2 . Пороговая энергия фотона для образования пары в поле электрона равна 4m e c 2 =2.044 МэВ.
Теоретические расчеты зависимости сечения рождения пар от энергии γ-квантов приводят к довольно сложному виду. Однако для области энергий 5m e c 2 < hν < 50m e c 2 эта зависимость может быть представлена в виде:

При энергии фотонов hν < 5m e c 2 и hν >50m e c 2 сечение растет медленнее. При hν > 50m e c 2 рост сечения ограничивается экранированием кулоновского поля ядра атомными электронами. В предельно релятивистском случае при hν > 10 3 m e c 2 сечение не зависит от энергии:

σ П ~ 0.08·Z 2 ·r e 2 = 0.63·10 -26 ·Z 2 cм 2 .

Общий характер зависимости сечения от энергии фотонов представлен на рис. 3.6.

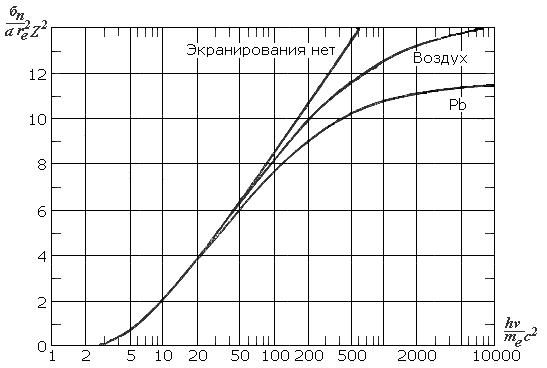
Рис.3.6 .Зависимость сечения рождения пар от энергии фотонов

Процесс рождения пар подобен процессу тормозного излучения. Поэтому выражения, описывающие эти два процесса, очень похожи по своей структуре: в случае полного экранирования вероятность того, что фотон с энергией Е« = hν на пути в 1 см образует электрон с энергией Е в интервале (E, E+dE) и позитрон с энергией (Е« − Е) будет:

Вероятность образования пары не зависит от энергии электрона Е и позитрона Е« − Е, и это понятно, так как в процессе их образования фотон исчезает и равновероятно распределение энергии между компонентами пары. Зная w n , можно найти полную вероятность образования пары на пути 1 см:

Таким образом, в случае полного экранирования полное сечение рождения пары не зависит от энергии фотона.

3.5. Другие процессы взаимодействия фотонов с веществом

1. Ядерный фотоэффект − поглощение γ-кванта ядром и испускание при этом нуклона, т.е. (γ,n)-реакция. Порог ядерного фотоэффекта -6-10 МэВ т.е. порядка энергии связи нуклонов в ядрах. Сечение ядерного фотоэффекта σ яф ~ Z и по величине существенно меньше сечений трех рассмотренных эффектов.

2. Если энергия фотонов много больше энергии связи нуклонов в ядрах, то может происходить фоторасщепление ядер с вылетом нескольких частиц. Например, (γ,2р), (γ,n,2р) — реакции. Сечение такого процесса σ я ~ 10 -26 см.

3. Если hν > 2m μ с 2 , т.е. hν > 200 МэВ, то в поле ядра γ-кванты могут образовывать μ − μ + -пары, аналогично е − е + -парам.

4. Если hν > m π с 2 , т.е. hν >140 МэВ, то может возникать фотогенерация пионов с сечением ~10 -28 А см 2 .

Таким образом, поглощение γ-квантов за счет всех перечисленных процессов пренебрежимо мало по сравнению с σ П.

3.6. Суммарное сечение взаимодействия фотонов с веществом

Ослабление потока фотонов при прохождении через вещество определяется главным образом тремя процессами: фотоэффектом, комптон-эффектом и образованием пар в кулоновском поле атомных ядер. Вследствие этого в формуле J = J0 e -σnx сечение о является суммой сечений этих процессов:
σ = σ ф + σ K + σ П, а линейный и массовый коэффициенты поглощения соответственно равны:
τ = σn = τ ф + τ K + τ П и μ = σn/ρ = μ ф + μ K + μ П. Каждое из слагаемых по-разному зависит от энергии фотонов и свойств вещества, поэтому относительная роль отдельных слагаемых может сильно меняться. Так, в алюминии (рис.3.7) в широком интервале энергий фотонов 50 кэВ < hν <15>15 МэВ − образование пар. В свинце же фотоэффект (рис.3.7) является доминирующим вплоть до энергии 0.5 МэВ, а при hν >5 МэВ основную роль играет процесс рождения пар.

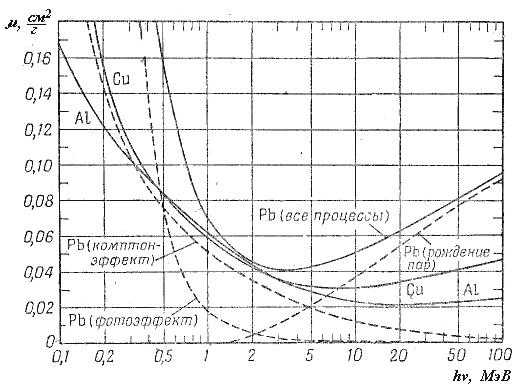
Рис.3.7. Зависимость массового коэффициента поглощения фотонов от их энергии в алюминии, меди и свинце

В заключение следует отметить важное обстоятельство: все три вида взаимодействия фотонов с веществом приводят к возникновению быстрых электронов.

3.7. Аннигиляция позитронов в веществе

Слово «аннигиляция» означает «исчезновение», «превращение в ничто». Это процесс, в котором частица и ее античастица превращаются в электромагнитное излучение (фотоны) или другие элементарные частицы (лептоны, кварки). Это процесс, обратный рождению пар γ-квантами. И тот и другой процессы − это просто взаимопревращения.
Эти взаимопревращения управляются фундаментальными законами сохранения: законом сохранения энергии, импульса, момента количества движения, электрического заряда и др.
Процессы рождения и аннигиляции частиц были теоретически предсказаны в 1931 г. П.А. Дираком . Они вытекали из созданной им теории электрона. Согласно Дираку, совместить квантовую механику (к тому времени уже подтвержденную экспериментом) с теорией относительности удается лишь, если наряду с состоянием электрона с положительной энергией ввести состояние электрона с отрицательной энергией (или положительного «электрона» с положительной энергией).
В 1932 г. К.Д. Андерсон , исследуя состав космических лучей с помощью камеры Вильсона, помещенной в магнитное поле, получил экспериментальные доказательства существования позитрона (Нобелевская премия, 1936 г.). По знаку кривизны следа частицы нашли, что частица положительная, а по изменению кривизны (после прохождения ею 6 мм свинца) и по плотности зерен в треке определили массу и импульс частицы. В 1933 г. Фредерик и Ирен Жолио-Кюри впервые получили фотографию камеры Вильсона со следами электрона и позитрона, рожденных гамма-квантом, и в том же году Ф. Жолио-Кюри впервые наблюдал аннигиляцию электронов и позитронов в два фотона.
Как же происходит аннигиляция позитронов? Попав в вещество, быстрые позитроны ведут себя так же, как и электроны, т.е. при Т е > ε они испытывают радиационное торможение, а при Т е < ε − ионизационные потери и, как правило, почти полностью теряют свою скорость. В дальнейшем начинается их диффузия в веществе до встречи со свободными или связанными в атомах электронами и последующая аннигиляция позитронов. Перед аннигиляцией обе частицы (электрон и позитрон) чаще всего находятся в состоянии, когда их моменты количества движения равны нулю (S-состояние). Дальнейшая судьба их зависит от взаимной ориентации внутренних моментов количества движения (спинов) и от того, свободен ли электрон или находится в связанном состоянии.
При встрече электрона и позитрона их полная энергия, включая энергию покоя, почти целиком переходит в энергию электромагнитного излучения (процесс, обратный рождению пар) и частично передается какому-то третьему телу, например, ядру. Если аннигиляция позитронов происходит на электроне, входящим в состав атома, то возможна аннигиляция с образованием одного фотона, т.к. импульс образующегося фотона будет компенсироваться отдачей атома или ядра, и закон сохранения импульсов будет выполняться. Законы сохранения энергии и импульса для этой ситуации можно записать так: + = ∑ t /c.

Замедлившийся до тепловой скорости позитрон может аннигилировать со свободным электроном, например, с одним из электронов проводимости в металле или с одним из внешних электронов атома. Если считать, что электрон и позитрон до аннигиляции покоились, то законы сохранения принимают вид:

2m е с 2 = ∑ t и 0 = ∑ t /c,

т.e. аннигиляция на свободном электроне возможна только при условии одновременного вылета не менее двух фотонов в противоположных направлениях. Поскольку обе аннигилирующие частицы с наибольшей вероятностью находятся в S-состоянии, то результат аннигиляции будет зависеть от взаимной ориентации внутренних моментов количества движения частиц, т.е. их спинов.
Если спины электрона и позитрона направлены в противоположные стороны (+1/2ћ и -1/2ћ), и, следовательно, их суммарный спин равен нулю, то в результате аннигиляции (согласно закону сохранения зарядовой четности) может образоваться лишь четное число фотонов со спинами, также направленными в противоположные стороны, т.к. спин каждого фотона равен l ћ. Так как вероятность аннигиляции w ~ α n , где n − число фотонов, то наиболее вероятно рождаются два фотона (w ~ α 2) -так называемая двухфотонная аннигиляция , менее вероятно − четыре фотона (w ~ α 4) и т.д.
Поскольку импульсы электрона и позитрона близки к нулю, то суммарный импульс системы тоже равен нулю, и, следовательно, образовавшиеся при аннигиляции фотоны летят в противоположные стороны, причем каждый из них забирает половину энергии системы, т.е. по 0.511 МэВ.
Если спины электрона и позитрона оказались параллельными, то их суммарный спин равен 1 ћ. В этом случае возможно образование нечетного числа фотонов, вероятнее всего − трех, так как один фотон возникнуть не может из-за невыполнения закона сохранения импульса. Вероятность трехфотонной аннигиляции ~ а 3 , т.е. существенно меньше (в 1/137 раз), чем двухфотонной. В среднем трехфотонная аннигиляция осуществляется в (0.2 — 0.3) % случаев.
Если аннигиляция происходит «на лету», т.е. в случае, когда позитрон еще не потерял скорость, то фотоны разлетаются под углом, причем угол разлета фотонов зависит от их скорости. При больших энергиях аннигилирующих позитронов возникшие фотоны испускаются преимущественно «вперед» и «назад» относительно направления движения позитрона. Фотон, летящий вперед, уносит большую часть энергии позитрона. На долю же фотона, летящего назад, остается минимальная энергия, т.е 0.511 МэВ. Поэтому при прохождении быстрых позитронов через вещество образуется пучок гамма-квантов, летящих в одном направлении, что используется для получения монохроматических пучков фотонов высокой энергии.
Позитрон − стабильная частица, в вакууме она существует бесконечно долго, но в веществе позитрон очень быстро аннигилирует. Среднее время жизни позитрона по отношению к процессу аннигиляции в твердых веществах составляет τ ~ 10 -10 с, а в воздухе при нормальных условиях τ ~10 -5 с.
Иногда аннигиляция идет через промежуточный этап, через образование связанного состояния электрона и позитрона, которое называется позитронием . Позитроний, в котором спины позитрона и электрона антипараллельны (парапозитроний), аннигилирует в два гамма-кванта со временем жизни
τ ~ 1.25·10 -10 с. Позитроний с параллельными спинами частиц (ортопозитроний) образует три гамма-кванта со временем жизни τ ~ 1.4·10 -7 с.
Явление аннигиляции позитронов сейчас широко используется для исследования свойств элементарных частиц. На встречных пучках позитронов и электронов в вакууме камеры ускорителя происходит процесс аннигиляции, в котором выделяется точно определенная энергия. Точечность взаимодействия и знание его энергии используется для доказательства существования кварков и определения их массы.

Вопросы и задачи к главе 3

1. Монохроматический пучок фотонов при прохождении алюминиевой пластины толщиной 2.9 см ослабляется в 2.6 раза. Определить τ, μ и σ.

До сих пор нейтрино было очень похоже на фотон. Подобно фотону, нейтрино не заряжено, не имеет массы, всегда движется со скоростью света. Обе частицы имеют спин. Спин фотона +1 или -1, тогда как спин нейтрино +1/2 или -1/2 (отличие не очень существенное). Тем не менее между ними существует интересная и даже удивительная разница, понять которую нам помогут следующие рассуждения.

Проследим два события, обращенные во времени. Пусть человек, держащий мяч, бросает его, скажем, на юг. Если же мяч приближается к человеку, двигаясь в обратном направлении, человек поднимает руку и ловит его. В первом случае последовательность событий была такова: 1) человек держит мяч, 2) человек бросает мяч, 3) мяч летит на юг. Движение, обращенное во времени, имело другую последовательность событий: 1) мяч летит на север, 2) человек ловит мяч, 3) человек держит мяч. Все это очень напоминает кинофильм, который сначала прокручивают в одну сторону, а затем в обратную.

Попробуем перенести этот принцип в субатомный мир Если электрон в атоме переходит из возбужденного состояния в менее возбужденное, он излучает фотон видимого света, длина волны которого зависит от разности энергий между двумя возбужденными состояниями атома. Тот же самый атом может поглотить или «поймать» фотон с точно такой же длиной волны, при этом электрон перейдет из менее возбужденного состояния в более возбужденное. Каждый тип атома излучает фотоны определенных длин волн (в зависимости от величины энергии его возбужденных состояний) и при подходящих условиях поглощает фотоны с точно такими же длинами волн.

И все-таки разница между прямым и обращенным во времени событием существует не только в изменении направления и последовательности. Поймать мяч труднее, чем бросить его. Бросая мяч, вы приводите в движение неподвижный предмет, и все зависит только от вас. Располагая своим временем, вы можете удобнее взять мяч, тщательно прицелиться и т. д. Когда же вы ловите мяч, приходится иметь дело с движущимся предметом и зевать некогда. Когда мяч приблизится, его нужно быстро схватить, так как мяч будет оставаться в пределах досягаемости долю секунды. В эту долю секунды вы должны успеть вытянуть руку точно в направлении движения мяча и остановить его. Если вы промахнетесь, мяч пролетит мимо.

То же самое происходит и с атомом, излучающим фотон. Такой атом испускает фотон за время, которое в среднем составляет около 10 -8 сек. Следовательно, атом, так сказать, сам распоряжается своим временем и излучает фотон, когда ему удобно.

Чтобы поглотить этот же фотон, атому необходимо 10 -8 сек, что является естественным следствием обратимости событий. Но атом не может поглотить фотон без значительных хлопот. Фотон движется со скоростью света и не остается вблизи атома в течение всего промежутка времени 10 -8 сек. За такой промежуток времени фотон света пролетает в среднем 300 см. Некоторые фотоны могут пройти большее расстояние, а другие меньшее. Понятно, почему обычно атомам очень трудно поймать фотоны: ведь размер атома значительно меньше этого расстояния! (Точно так же баскетболистам трудно ловить мячи, летящие слишком быстро). Тем не менее, случайно атом может поймать и поглотить фотон.

Все сказанное предполагает, что фотон не имеет собственных размеров; хотя на самом деле его размеры довольно велики. Типичный фотон видимого света имеет длину волны около 1/20 000 см. На этой длине укладывается в ряд около тысячи атомов. Фотон видимого света можно представить как некую сферу, диаметр которой в тысячу раз больше диаметра атома, а объем в 1000000000 раз больше объема атома. В любой момент времени фотон света соприкасается приблизительно с миллиардом атомов, один из которых ухитряется поймать и поглотить его.

Следовательно, глубина, на которую фотон проникает в вещество до поглощения, не 300 см, а в миллиард раз меньше, т. е. 3·10 -7 см.

На таком расстоянии умещаются в ряд не более 10–15 атомов. Это означает, что фотон света до момента поглощения проникает в вещество не глубже, чем на 10–15 атомарных слоев. Толщина в 10–15 атомов — сущий пустяк в обычных масштабах, поэтому большинство твердых веществ даже в виде тонких пленок непрозрачны для света (хотя золотую фольгу можно сделать настолько тонкой, что она станет прозрачной).

Чем короче длина волны света, тем меньше фотон, тем меньше атомов соприкасается с ним в любой момент времени и, следовательно, тем больший путь он проходит через вещество до поглощения. Именно по этой причине ультрафиолетовый свет проникает в кожу человека глубже, чем видимый свет; рентгеновские лучи свободно проходят через мягкие ткани тела и останавливаются только более плотным веществом костей; а?-лучи пронизывают плотное вещество на много сантиметров. (Конечно, видимый свет проходит значительное расстояние в таких веществах, как стекло или кварц, не говоря уже о большинстве жидкостей, но все это является предметом отдельного рассмотрения).

Поглощение нейтрино Постараемся теперь использовать все вышесказанное применительно к нейтрино и антинейтрино. Запишем еще раз реакцию распада нейтрона, в результате которой образуется протон, электрон и антинейтрино: п > р + + е — + «?. Предположим, что при подходящих условиях возможен обратный процесс, в котором протон, захватывая электрон и антинейтрино, становится нейтроном. Тогда обратная реакция выглядела бы так: р + + е — + «? > п. Естественно, протон должен поймать электрон и антинейтрино одновременно, что очень сильно уменьшает вероятность успешного завершения процесса. (Это равносильно тому, чтобы просить баскетболиста поймать одной рукой одновременно два мяча, летящих на него с разных сторон.) Для упрощения задачи изменим порядок обращения. Любой процесс, в котором происходит поглощение электрона, можно заменить процессом, в результате которого рождается позитрон. (Подобное правило существует в алгебре: вычитание -1 равносильно прибавлению +1.) Другими словами, вместо одновременного поглощения электрона и антинейтрино протон может поглотить антинейтрино и излучить позитрон: р + + «? > п + «е+. При таком варианте реакции законы сохранения выполняются. Поскольку протон заменяется нейтроном (оба с барионным числом +1), а антинейтрино заменяется позитроном (оба с лептонным числом -1), законы сохранения барионного и лептонного чисел выполняются. Остается рассмотреть вероятность поглощения антинейтрино протоном. Период полураспада нейтрона равен 12,8 мин, хотя отдельным нейтронам для распада требуется больше или меньше 12,8 мин. Следовательно, для образования нейтрона при захвате протоном антинейтрино и излучении позитрона требуется в среднем 12,8 мин . Другими словами, антинейтрино поглощается протоном в среднем за 12,8 мин. Но нейтрино распространяется со скоростью света и за 12,8 мин проходит расстояние 2,3·10 8 км (т. е. путь, приблизительно равный расстоянию от Солнца до Марса). Трудно поверить, что антинейтрино до поглощения способно пройти такое огромное расстояние в твердом веществе, даже если предположить, что объем его равен объему фотона. Но на самом деле антинейтрино значительно меньше атома. В действительности дело обстоит гораздо сложнее, В случае фотонов поглощение происходит за счет электронов, занимающих большую часть объема атома, а в твердом веществе атомы плотно прилегают друг к другу. Антинейтрино же поглощается протонами, расположенными в атомных ядрах, которые занимают ничтожную часть атома. Антинейтрино, пролетая через твердое вещество, очень редко сталкивается с крошечным ядром. Лишь одну стомиллионную всего времени, в течение которого антинейтрино находится внутри атома, оно бывает настолько близко к протону, что последний может захватить его. Следовательно, для того чтобы у антинейтрино был определенный шанс быть пойманным протоном, оно должно пройти в твердом веществе путь в сто миллионов раз больший, чем 230 000 000 км. Было установлено, что в среднем антинейтрино должно пролететь в свинце около 3500 световых лет до поглощения. Естественно, во Вселенной нигде нет слоя свинца толщиной в 3500 световых лет. Вселенная состоит из отдельных звезд, чрезвычайно редко распределенных в пространстве, а диаметр любой звезды значительно меньше одной миллионной светового года. Большинство звезд состоят из вещества, плотность которого значительно меньшей плотности свинца. Исключение составляет сверхплотное вещество сравнительно небольшого ядра звезды. (Во Вселенной имеются и сверхплотные звезды, но они очень малы — не больше планет.) Но задержать антинейтрино не могут даже сверхплотные части звезд. Пролетая через Вселенную в любом направлении, антинейтрино очень редко проходит сквозь звезду и еще реже — сквозь ее сверхплотное ядро. Суммарная толщина звездного вещества, через которое проходит антинейтрино, пролетая из одного конца видимой Вселенной в другой, значительно меньше одного светового года. Все, что говорилось здесь относительно антинейтрино, применимо, естественно, к нейтрино, и можно, следовательно, утверждать, что нейтрино и антинейтрино практически не поглощаются. Однажды возникнув в каком-то субатомном процессе, они вечно движутся и не подвержены никаким изменениям и влияниям со стороны всего окружающего. Время от времени они поглощаются, но число поглощенных нейтрино ничтожно по сравнению с огромным числом уже существующих и вновь возникающих. Современные знания позволяют нам с уверенностью сказать, что фактически все нейтрино и антинейтрино, возникшие за время жизни Вселенной, существуют и по сей день.

Как же поймали антинейтрино?

Сделанный выше вывод явился не очень приятной новостью. Сколько бы ни выводил физик необходимость существования нейтрино и антинейтрино из законов сохранения, он был бы по-настоящему счастлив, только действительно обнаружив крошечные частицы прямым наблюдением. Но, чтобы продемонстрировать их существование, он должен сначала поймать хотя бы одну частицу, то есть заставить ее провзаимодействовать с какой-нибудь другой частицей, чтобы можно было обнаружить результат этого взаимодействия. А поскольку поймать нейтрино или антинейтрино фактически было невозможно, возникло серьезное сомнение в реальности их существования!

В результате физик спас свое представление о строении Вселенной, которое развивалось на протяжении трех столетий, настаивая на существовании чего-то, что нужно было принять на веру. Он доказывал существование нейтрино на основе своих теорий и спасал свои теории, утверждая существование нейтрино. Получился «замкнутый круг». Причины для сомнений и неопределенности оставались. Было чрезвычайно важно разработать какой-нибудь метод регистрации нейтрино или антинейтрино, если это вообще возможно.

Брешь в почти непроницаемой броне неуловимого нейтрино была пробита с помощью слова «в среднем». Я говорил, что до поглощения антинейтрино в среднем проходит через слой твердого свинца толщиной 3500 световых лет. Но это только в среднем. Некоторые антинейтрино, возможно, проходят более короткий путь, другие — более длинный, и лишь немногие пройдут до поглощения или очень маленькое, или очень большое расстояние. Следовательно, необходимо сосредоточить внимание на бесконечно малой доле антинейтрино, поглощающихся в такой толщине вещества (скажем, несколько метров), которую легко создать в лаборатории. Чтобы этот бесконечно малый процент содержал возможно большее число антинейтрино, необходимо иметь очень мощный источник этих частиц. Таким мощным источником антинейтрино является ядерный реактор. Образующиеся в реакторе избыточные нейтроны рано или поздно распадаются на протоны, электроны и антинейтрино. Когда реактор работает на полную мощность, непрерывно рождается огромное число антинейтрино. В 1953 году группа американских физиков, возглавляемая Клайдом Коуэном и Фредериком Рейнесом, начала опыты по регистрации антинейтрино. В качестве источника частиц они использовали ядерный реактор в Саванна-Ривер, штат Южная Каролина. Этот реактор испускал каждую секунду примерно 10 18 антинейтрино.

Рис. 7. Детектирование антинейтрино.

Для такого несметного числа антинейтрино нужно было создать мишень, богатую протонами. Простейшей естественной мишенью является вода. Каждая молекула воды состоит из двух атомов водорода, ядра которых представляют собой протоны, и атома кислорода. Коуэн и Рейнес использовали пять баков воды длиной 1,9 м и шириной 1,4 м. Толщина баков была различной (рис. 7). Два тонких бака высотой 7,6 см использовались в качестве мишени. Три других бака высотой 60 см служили детектором. Баки располагали в таком порядке: детектор — мишень — детектор — мишень — детектор. Вода в баках-мишенях содержала небольшое количество растворенного хлористого кадмия. Баки-детекторы содержали раствор сцинтиллятора — вещества, которое излучает часть энергии, полученной им при поглощении субатомной частицы, в виде короткой вспышки света. Такой «двойной сэндвич» из баков располагался на пути потока антинейтрино из реактора. Оставалось только ждать. Если антинейтрино действительно существуют, каждые Двадцать минут (в среднем) одно из них должно поглотиться протоном. Но баки подвергались непрерывному действию космического излучения из межпланетного пространства, бомбардировке частицами, испускаемыми небольшими количествами радиоактивных веществ, находящихся в воздухе, строительных материалах, почве. Вся трудность заключалась в том, чтобы на всем этом фоне событий, происходивших внутри баков с водой, выделить поглощение антинейтрино.

Вначале нежелательный субатомный «шум» не позволял обнаружить поглощение антинейтрино. Постепенно создавалось все более и более эффективное экранирование, чтобы избавиться от нежелательного излучения и частиц. Конечно, антинейтрино никакое экранирование, никакие толщины металла или бетона не могли задержать, и в конце концов «шум» уменьшился до уровня, который уже не скрывал слабый «шепот» очень редких антинейтрино, случайно захваченных протонами. Но этот шепот надо было еще идентифицировать.

При поглощении антинейтрино протоном образуется нейтрон и позитрон — комбинация частиц, которую легко отличить. Как только в одном из баков-мишеней образуется позитрон, он взаимодействует с электроном меньше, чем за одну миллионную секунды, при этом возникает два фотона, каждый из которых имеет энергию 0,51 МэВ . Согласно закону сохранения импульса, два фотона должны разлетаться в точно противоположных направлениях: если один из них из бака-мишени попадает в верхний бак-детектор, то другой должен попасть в нижний бак-детектор. В каждом баке-детекторе возникает вспышка света. Эти вспышки тотчас же автоматически регистрируются сотней или более фотоумножителей, расположенных вокруг баков с водой.

А что же происходит с нейтроном? Обычно он просто блуждает среди молекул воды (которые очень редко поглощают нейтрон), сталкиваясь с ними, пока самопроизвольно не распадется в среднем через 12,8 мин после своего возникновения. Однако ждать так долго ни к чему, так как распад может произойти на несколько минут раньше или позже. Вот здесь-то и приходит на помощь хлористый кадмий в баке-мишени. Нейтрон блуждает до тех пор, пока не столкнется с атомом кадмия, тогда он почти мгновенно поглощается. Происходит это в течение нескольких миллионных долей секунды после аннигиляции позитрона — срок довольно короткий и все же достаточный, чтобы разделить во времени два события: аннигиляцию позитрона и поглощение нейтрона. При поглощении нейтрона атомом кадмия выделяется энергия, которая тотчас излучается в виде трех или четырех фотонов с суммарной энергией 9 Мэв.

Итак, Коуэн и Рейнес наблюдали следующую картину: сначала одновременно появлялись два фотона с энергией 0,5 Мэв каждый, которые регистрировались двумя фотоумножителями на противоположных сторонах баков с водой, затем через несколько миллионных долей секунды следовало одновременное образование трех фотонов с энергией 3 Мэв каждый (иногда четырех фотонов с энергией 2,25 Мэв каждый). Никакое другое субатомное взаимодействие не приводило к такой последовательности событий. И если был зарегистрирован именно такой ход событий, разумно было заключить, что протон поглощает антинейтрино, следовательно, антинейтрино действительно существует.

Но тут в осторожных умах экспериментаторов возникла другая мысль. А что если такая последовательность событий вызвана не одним субатомным взаимодействием, а двумя?

Предположим, что каким-то образом возник позитрон, а через несколько миллионных долей секунды атом кадмия поглотил нейтрон, который существовал независимо от позитрона. В таком случае появление двух, а затем трех фотонов явилось бы результатом не одного взаимодействия (антинейтрино с протоном), а двух совершенно несвязанных взаимодействий. Какое же взаимодействие наблюдали Коуэн и Рейнес?

Экспериментаторы решили проблему, произведя свои измерения сначала с работающим реактором, а затем с выключенным. Если реактор выключить, на баки будет действовать шум, а бомбардировка их потоком антинейтрино прекратится. (На самом деле в окружающем пространстве всегда имеются антинейтрино, но их число намного меньше числа антинейтрино вблизи работающего реактора.) Следовательно, при выключенном реакторе продолжали бы регистрироваться двойные совпадения, а поглощение антинейтрино прекратилось бы.

Оказалось, что с выключенным реактором регистрировалось на 70 событий в день меньше, чем с включенным. Значит, в день поглощалось и регистрировалось 70 антинейтрино (по одному каждые двадцать минут). Результаты эксперимента можно было считать несомненным доказательством, и в 1956 году было сделано сообщение, что спустя целых двадцать пять лет после того, как Паули впервые предсказал существование антинейтрино, такая частица была наконец зарегистрирована. Об этом событии обычно говорят как о «регистрации нейтрино», хотя было зарегистрировано антинейтрино. Однако после того, как «изловили» антинейтрино, физики считают, что существование нейтрино не вызывает сомнения.

Основным процессом, к которому приводит поглощение электромагнитного излучения в полупроводниках, является генерация электронно – дырочных пар. При поглощении фотонов с энергиями возможны прямые переходы электронов через запрещённую зону (здесь h – постоянная Планка, 6,63*10 -34 Дж*с; ν – частота излучения; Е g – ширина запрещённой зоны; полупроводниковые материалы солнечных элементов имеют Еg= 1эВ). h*ν > E g (7.1.)

Солнечное излучение характеризуется высокой плотностью потока фотонов (1кВт/м 2 /[(2эВ)*(1,6*10 -19 Дж*эВ -1)] ≈ 3*10 21 фотон/м 2 *с). Генерация носителей фотонами при освещении Солнцем полупроводника суммируется с всегда с присутствующей термической генерацией. В темноте существует только термическая генерация. Поглощающий фотоны р- n переход является источником постоянного тока. Фототок определяется количеством фотонов, поглощённых вблизи р – n перехода. Минимальная величина солнечного элемента из кремния =0,4мм. Фотоэлементы можно использовать для получения электроэнергии. Максимум энергии достигается, если поддерживать напряжение U и ток I такими, чтобы их произведение совпадало с линией максимальной мощности (рис. 7.1.) при изменении облучённости и сопротивлении нагрузки.

Рис. 7.1. Вольт – амперная характеристика типичной солнечной батареи из 33 кремниевых элементов. Видно, что линия типовой мощности (штриховая линия), соответствующая максимуму произведения U*I, хорошо согласуется с областью напряжений, требуемых для зарядки аккумуляторных батарей, даже без использования контроля нагрузки.

Батарея солнечных элементов представляет собой комбинацию соединённых параллельно модулей. Каждый модуль представляет собой последовательно соединённые элементы. Полное КПД солнечного элемента – 10%.

Существует много вариантов и промышленных разработок фотоэлементов и методов их изготовления. Стандартный солнечный монокристаллический кремниевый элемент показан на рис. 7.2.

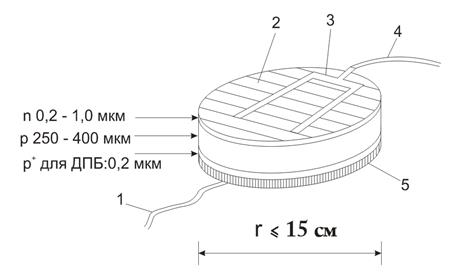
Рис. 7.2. ДПБ – добавочный потенциальный барьер; 1- от лицевой поверхности предыдущего элемента; 2 – противоотражательное покрытие; 3 – лицевой контакт; 4 – к тыльному контакту следующего элемента; 5 — металлический контакт с тыльной стороны.

Основные технические требования

1. Исходный материал должен быть химически высоко чистым с устойчивыми свойствами.

2. Фотоэлементы должны производиться при минимальной стоимости.

3. Солнечные элементы должны иметь срок службы не менее 20 лет в условиях воздействия окружающей среды. Следует учитывать, что рабочая температура фотоэлемента может меняться в диапазоне от (- 30) до +200 0 С.

4. Электрические контакты должны быть стабильными и защищёнными от всех видов коррозии. Устройство должно быть водозащищённым.

5. Разрушение одного из элементов не должно приводить к выходу из строя всей системы.

6. Сборные модули должны выдерживать транспортировку в труднодоступные районы.

Энергия ветра

Причиной возникновения ветра является поглощение земной атмосферой солнечного излучения, что приводит к расширению воздуха, появлению мощных вертикальных и более слабых горизонтальных потоков.

Характер течений определяется как местными географическими факторами, так и вращением Земли. На Земле ветры подразделяются на глобальные и местные.

К глобальным ветрам относятся пассаты и западный ветер. Пассаты образуются в результате нагрева экваториальной части Земли. Нагретый воздух поднимается вверх, увлекая за собой воздушные массы с севера и юга. Вращение Земли отклоняет потоки воздуха. В результате устанавливаются дующие круглый год с постоянной силой северо – восточный пассат в северном полушарии и юго – восточный в южном. Пассаты дуют в приэкваториальной области, заключённой между 25 и 30 0 северной и южной широтами соответственно. В северном полушарии пассаты охватывают 11% поверхности океанов, а в южной 20%. Сила пассатного ветра обычно составляет 2 – 3 балла. Западный ветер дует круглый год с запада на восток в полосе от 40 до 60 0 южной широты вдоль кромки дрейфующих льдов Антарктиды. Это самый сильный постоянный ветер. Его сила достигает 8 – 10 баллов и редко бывает менее 5 баллов. В глубине материка нет постоянного направления ветра. Так как разные участки суши в разное время года нагреваются неодинаково, можно говорить только о преимущественном сезонном направлении ветра. Кроме того, на разной высоте ветер ведёт себя по – разному, а для высот до 50 метров характерны «рыскающие» потоки.

Местные ветры первыми использовались для плавания. К ним относятся бризы. Бризы – это лёгкие ветры, окаймляющие берега материков и больших островов, вызываемые суточным колебанием температуры. Их периодичность обусловлена различием температуры суши и моря днём и ночью. Днём суша нагревается быстрее и сильнее, чем море. Тёплый воздух поднимается над береговой полосой, а на его место устремляется прохладный воздух с моря – морской бриз. Ночью берег охлаждается быстрее и сильнее, чем море, поэтому тёплый воздух поднимается над морем, а его замещает холодный воздух с суши – береговой бриз. Вторыми, постоянно дующими ветрами, являются муссоны. Эти ветры дуют в Индийском океане и связаны с сезонным изменением температуры материка и океана. Летом солнечные лучи сильнее нагревают сушу, и ветер дует с моря на сушу. Зимой муссон дует с суши на море. Вращение Земли вызывает появление сил Кориолиса, которые отклоняют муссоны вправо. Поэтому летом дуют юго – западные муссоны, а зимой – северо – восточные. Муссоны достигают большой силы и вызывают в Индийском океане соответствующие местным ветрам поверхностные течения.

Таблица 8.1.

Сила ветра по шкале Бофорта

Балл по шкале	Скорость ветра, м/с	Название ветра	Наблюдаемый эффект	Воздействие на ВУ (работа)	Условия работы ВУ

	0 – 0,4	Штиль	Дым из труб поднимается вертикально	Нет	Нет
	0,4 – 1,8	Тихий	Дым поднимается отвесно	Нет	Нет
	1,8 – 3,6	Лёгкий	Шелестят листья	Нет	Нет
	3,6 – 5,8	Слабый	Колеблются листья	Удовлетворительное	Начинают вращаться тихоходные колёса
	5,8 – 8,5	Умеренный	Колеблются тонкие ветки	Хорошее	Вращаются колёса электрогенераторов
	8,5 — 11	Свежий	Начинают раскачиваться лиственные деревья	Очень хорошее	Мощность 30%
	11 — 14	Сильный	Качаются большие ветки	Приемлемое	Полная мощность


14 — 17	Крепкий	Все деревья раскачиваются	Предельное	Максимально допустимая мощность
17 — 21	Очень крепкий	Ломаются ветки, трудно идти	Недопустимые условия	Роторы отключаются
21 — 25	Шторм	Разрушения	Недопустимые условия	Отключаются все энергетические установки
25 — 29	Сильный шторм	Деревья вырываются с корнем	Недопустимые условия	Предельные нагрузки
29 — 34	Жестокий шторм	Широкомасштабные разрушения	Недопустимые условия	Сверхрасчётные нагрузки
>34	Ураган	Опустошительные разрушения	Недо0,45 условия	Разрушения

При скорости ветра u o и плотности воздуха ρ ветроколесо, ометающее площадь А, развивает мощность.

Поглощение фотонов

Лекция: Постулаты Бора. Излучение и поглощение фотонов при переходе атома с одного уровня энергии на другой

Несмотря на столь удачное открытие Резерфорда касательно модели атома, она столкнулась с некоторыми сложностями, которые смог растолковать Н.Бор.

Итак, нам уже известно, что электрон, которому придали ускорение, начинает излучать — это утверждение было выдвинуто Максвеллом. И это было не просто утверждение, а известный факт, которого стоило считаться. Так же нам известно, что любая частица, которая двигается с ускорением, тратит некоторую энергию, которая может пополниться только с помощью дополнительных условий.

Придерживаясь данной логики, можно сделать вывод, что любой электрон, который двигается по орбите, постоянно меняет направление своей скорости, а это значит, что он имеет ускорение. Стало быть, любой электрон, вращаясь вокруг ядра, должен постоянно терять энергию, и в конечном итоге упасть на ядро. Однако, этого вокруг не происходит. А значит, что-то не учтено.

Если использовать знания из динамики Ньютона, а также наблюдений Максвелла, можно сделать вывод, что электроны практически моментально теряют всю свою энергию, в результате чего существование каждого атома должно быть не более 10 -7 с, что на самом деле не так.

Постулаты Бора

Исходя из всего описанного, и того, что вокруг нас не происходит постоянного разрушение всех предметов, можно сделать вывод, что законы механики не справедливы для микромира. А что на самом деле происходит в атоме, мы рассмотрим прямо сейчас.

Описать, что происходит в атоме гидрогена, рискнул ученый Н.Бор, который предложил несколько правил (постулатов), которые неким образом отличались от всех известных законов, но смогли объяснить некоторые процессы в атоме. С помощью привычных законов можно описать практически все видимые явления, которые происходят вокруг нас — движение тела, изменение состояния газов, а также многое другое. Однако ни в одном из данных процессов энергия не рассматривалась в качестве порции. А так как мы знаем, что в результате движения частицы происходит излучение спектров, то энергия рассматривается в качестве парциальной величины, кратной энергии фотона. Именно поэтому для рассмотрения процессов в атомах следовало это учитывать.

Первый постулат:

Электрон может находиться на некоторой стационарной орбите, которой соответствует своя энергия. То есть, именно от энергии, которой обладает электрон, зависит, на какой орбите он может находиться или даже вырваться с нее.

Первый постулат гласит, что находясь на стационарных орбитах, атом не излучает.

Данный постулат звучит вполне сказочно, однако в начале 20 века стационарные состояния были доказаны Франком и Герцем. В зависимости от имеющегося набора энергий, электроны находятся на некоторых орбитах. Однако, из химии нам известно, что электроны могут перескакивать между орбитами. Как это происходит?

Второй постулат:

В то время, когда электрон перемещается между стационарными орбитами, происходит выделение или поглощение энергии. То есть при переходе орбиты с большей энергией на орбиту с меньшей энергией, происходит излучение. Если же некоторый фотон налетает на электрон, тот полностью поглощает его. В результате этого происходит обратное перемещение электрона между орбитами.

Итак, например для того, чтобы электрон перешел с третьей орбиты на вторую, должно произойти излучение энергии, которую можно найти по формуле, указанной на рисунке:

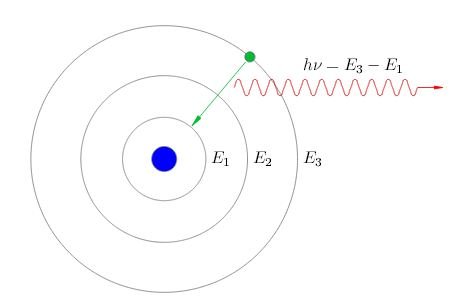
Это позволяет понять причину того, что спектры в результате излучения атомами, являются линейчатыми. Стоит отметить, что величины энергий, которые поглощаются или излучаются в результате перехода электрона между уровнями, должны быть кратный элементарной энергии данного атома.

Третий постулат Бора:

Данный постулат позволяет определить природу квантования. Он говорит о том, что электрон может обладать моментом импульса, который будет прямо пропорционален перечеркнутой постоянной Планка: