Как разгадывать ребусы. Вопросы для повторения Ветка ветка дерево решение ребуса
Ознакомившись с правилами как разгадывать ребусы, вы сможете без особого труда не только разгадать любой ребус, но и узнаете как составить ребус самому.
- Название всего, что изображено на картинках в ребусе, читается только в именительном падеже.
- Картинка в ребусе может иметь не одно название. Пример: нога и лапа, глаз и око; или изображение может иметь общее или частное название (птица — общее название; петух, голубь, чайка — частное название).
- Запятые (не имеет значения, перевёрнутые или нет) указывают, что из слова следует убрать крайние буквы. Сначала слова, если запятые стоят перед картинкой, или с конца слова, если запятые после картинки. Количество букв, которые нужно убрать, соответствует количеству запятых. ЛЕС
- Зачёркнутые буквы — такие буквы следует убрать из слова. Если зачёркнутые буквы повторяются, то они убираются все.
 КАССА
КАССА - Зачёркнутые цифры указывают, что в слове такую по счёту букву надо убрать.
- Знак равенства между буквами (А=Е) указывает, что нужно заменить все буквы А на Е. Равенство 1=Е указывает на замену только первой буквы в слове.
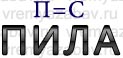 СИЛА
СИЛА - Стрелка между буквами (Е -> В) тоже указывает на соответствующую замену букв.
- Цифры 1,2,7,5 над картинкой указывают, что из данного слова нужно взять буквы под номерами 1,2,7,5 и составить их в том порядке, в котором расположены цифры.
 ТАНК
ТАНК - Перевёрнутый вверх ногами рисунок указывает, что слово следует читать справа налево. (КОТ — ТОК)
- Стрелка, остриём влево, изображённая над картинкой указывает, что после того как слово разшифровано его нужно прочитать задом наперёд.
 КОТ
КОТ - Когда в ребусе используется дробь, это разгадывается как «НА» (разделить НА). Если же в ребусе используется дробь со знаменателем 2, то это разгадывается как «ПОЛ» (половина).
 ПОЛКА
ПОЛКА  ФОНАРЬ
ФОНАРЬ - При составлении ребусов используют ноты. Для определения ноты имеет значение только то, на какой черте расположена чёрная точка (нота).

- Внутри буквы «О» расположен слог «ДА», получается В-О-ДА, т.е. «ВОДА». Также это можно прочитать как «ДА-В-О». Выбирается вариант, подходящий по смыслу.
 ВОЛЯ
ВОЛЯ - Когда картинки расположены друг над другом, это читается как «НАД», «НА», «ПОД» (в зависимости от того, что подходит по смыслу).
 ПОДАРОК
ПОДАРОК  АНАНАС
АНАНАС - Буква, состоящая из других букв, читается как предлог «ИЗ». Например из буквы «Б» составим букву «А», то получим: из «Б» «А» (ИЗБА). ИЗБА
- Буква, расположенная поверх другой буквы, читается как «ПО». ПОЛЕ
- Буква, изображённая за другой буквой, читается как предлог «ЗА» или «ПЕРЕД». Выбирается вариант, подходящий по смыслу.
 ЗАЯЦ
ЗАЯЦ - Знак «+» означает предлог «К» (Прим. 2+3 можно прочитать: К Двум прибавить Три или Три прибавить К Двум). Следует выбирать вариант подходящий по смыслу.
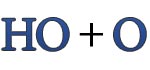 ОкНО
ОкНО 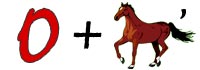 кОкон
кОкон - Двойная стрелка между цифрами означает, что буквы под этими номерами нужно поменять местами друг с другом.
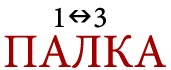 Лапка
Лапка - Перечёркнутый знак «=» между картинками следует читать как «НЕ» (Пример: «С» НЕ равно «Г»).
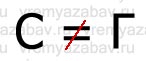 СнеГ
СнеГ
Ну что теперь вы готовы решить любой ребус?
P.S.: Если вы знаете ещё какие-нибудь правила для разгадывания ребусов или заметили какую-то неточность в описании имеющихся правил, то напишите, пожалуйста об этом в комментариях ниже.
{jcomments on}
Назовём такой метод — контролируемый перебор.
program zadacha3_8c;
for k:=1 to 4 do
for t:=2 to 9 do
if k<>t then
for o:=0 to 9 do
if (k<>o) and (t<>o) then
kto:=k*100+t*10+o;
kot:=k*100+o*10+t;
tok:=t*100+o*10+k;
if kto+kot=tok then writeln(kto,»+»,kot,»=»,tok);
Такой алгоритм даже при 8-10 вложенных циклах работает очень быстро.
Вопросы для повторения :
1. Может ли во вложенных циклах использоваться одна и та же переменная, например i?
2. Можно ли вкладывать друг в друга различные циклы: FOR в WHILE или REPEAT в FOR?
Задания для самостоятельной работы :
1. Старинная задача. Сколько можно купить быков, коров и телят, если бык стоит 10 рублей, корова – 5 рублей, телёнок – полтинник (0,5 рубля), при условии, что на 100 рублей надо купить 100 голов скота.
2. Задано натуральное n. Для всех чисел от 1 до n найти:
a) количество делителей; b) сумму чётных делителей.
3. Найти все решения следующих числовых ребусов:
a) БАБКА+ДЕДКА+РЕПКА=СКАЗКА (4 решения)
b) КОРОВА+ТРАВА+ДОЯРКА=МОЛОКО (2 решения)
c) АЛЁНКА+ИВАН+КОЗЛИК=СКАЗКА (1 решение)
d) ВЕТКА+ВЕТКА+СТВОЛ=ДЕРЕВО (3 решения)
e) ВОРОТА+ТРАВА=ФУТБОЛ (3 решения)
Изучаем “Циклы”
М4_Блок № 3
Тема урока :
Вложенные циклы.
Цель занятия :
1. Закрепить знания по использованию различных типов циклов;
2. Получить навыки решения алгоритмов с вложенными циклами.
СШ №1 г. Лида
Для решения задачи достаточно часто требуется использовать несколько вложенных друг в друга циклических конструкций. Такие конструкции называют вложенными циклами.
Рассмотрим несколько примеров:
Дано натуральное число S . Требуется написать программу для нахождения всех прямоугольников, площадь которых равна S и стороны выражены натуральными числами.
program zadacha3_6;
var s, a, b:longint;
writeln(«Введите s»); readln(s);
for a:=1 to s do
for b:=1 to s do
if a*b=s then writeln («стороны «,a,» и «,b);
Данную задачу можно было решить, используя только один цикл. Подумайте, как это сделать.
Даны натуральные числа n , m . Получить все натуральные числа, меньшие n , сумма квадратов цифр которых равна m .
program zadacha3_7;
var n, m, i, a, sum, cif:longint;
writeln(«введите n и m»);readln(n, m);
for i:=1 to n do
sum:=sum+sqr(cif);
if sum=m then write(i,» «);
Найти все решения заданного числового ребуса. Каждой букве соответствует некоторая цифра. Причём одинаковым буквам соответствуют одинаковые цифры, разным буквам — разные цифры.
Поскольку здесь всего три буквы, то для решения достаточно написать три вложенных цикла, и перебрать все варианты сложения трёхзначных чисел.
program zadacha3_8a;
var k, t, o, kto, kot, tok:longint;
for k:=0 to 9 do
for t:=0 to 9 do
for o:=0 to 9 do
kto:=k*100+t*10+o;
kot:=k*100+o*10+t;
tok:=t*100+o*10+k;
if (k<>t) and (k<>o) and (t<>o) and (kto+kot=tok) then
writeln(kto,»+»,kot,»=»,tok);
В данном алгоритме тело цикла выполнялось 10∙10∙10=1000 раз. (будем говорить сложность алгоритма =1000)
Если же для решения более сложных ребусов потребуется написать 8-10 вложенных циклов, то такой полный перебор будет работать достаточно долго.
Можно немного упростить данный алгоритм, если увидеть что 1≤k≤4, t≥2.
for k:=1 to 4 do
for t:=2 to 9 do
for o:=0 to 9 do
Теперь сложность алгоритма 4∙8∙10=320. Простое косметическое исправление дало увеличение скорости в 3 раза.
Но и данный алгоритм не является оптимальным. Посмотрите, при k =2 и t =2 программа переберёт все 10 вариантов o . В таких случаях когда k =t цикл по o вообще необходимо не выполнять.
