Связь между ускорением и силой кратко. Сила (физическая величина). Явления, связанные с движением заряда

3 мая 2020

Движение всех окружающих нас макроскопических объектов описывается с помощью так называемых трех законов Ньютона. В данной статье не будем говорить ничего о первых двух из них, а рассмотрим подробно третий закон Ньютона и примеры его проявления в жизни.

Формулировка закона

Каждый из нас замечал, что при прыжке на какую-либо поверхность она будто бы «ударяет» по нашим ногам, или же если взяться за руль велосипеда, то он начинает давить на ладони. Все это примеры третьего закона Ньютона. В курсе физики в общеобразовательных школах он формулируется следующим образом: любое тело, оказывающее силовое воздействие на некоторое другое тело, испытывает аналогичное воздействие от последнего, направленное в противоположную сторону.

Математически этот закон может быть записан в следующем виде:

В левой части равенства записана сила, с которой первое тело действует на второе, в правой части стоит аналогичная по модулю сила, с которой второе тело воздействует на первое, но уже в противоположном направлении (поэтому появляется знак минуса).

Равенство модулей и противоположное направление рассмотренных сил привели к тому, что этот закон часто называют взаимодействием, или принципом воздействия-противодействия.

Действие на различные тела — ключевой момент рассматриваемого закона

Взглянув на представленную выше формулу, можно подумать, что раз уж силы по модулю равны, а по направлению противоположны, то зачем вообще их рассматривать, ведь они аннулируют друг друга. Это суждение является ошибочным. Доказательством этого является огромное количество примеров третьего закона Ньютона из жизни. Например, лошадь тянет телегу. Согласно рассматриваемому закону лошадь воздействует на телегу, но с такой же силой последняя действует на животное в противоположном направлении. Тем не менее вся система (лошадь и телега) не стоит на месте, а движется.

Приведенный пример показывает, что рассматриваемый принцип действия-противодействия не является таким простым, как это кажется на первый взгляд. Силы F 12 ¯ и -F 21 ¯ не аннулируются, поскольку приложены они к разным телам. Лошадь не стоит на месте, хотя телега и препятствует этому, только потому, что на ее копыта действует еще одна сила, которая и стремится сообщить ускорение животному — это воздействие поверхности земли (реакция опоры).

Таким образом, при решении задач на 3-й ньютоновский принцип следует всегда рассматривать силы, которые действуют на отдельные конкретные тела, а не на всю систему сразу.

Связь с законом сохранения количества движения

Третий ньютоновский закон по сути является причиной сохранения импульса системы. Действительно, рассмотрим один интересный пример третьего закона Ньютона — движение ракеты в космическом пространстве. Всем известно, что оно осуществляется за счет реактивной тяги. Но откуда берется эта тяга? Ракета несет на своем борту баки с топливом, например с керосином и кислородом. Во время сгорания топливо покидает ракету и вылетает с огромной скоростью в космическое пространство. Этот процесс характеризуется воздействием сгоревших газов на корпус ракеты, последний же оказывает воздействие на газы с аналогичной силой. Результат проявляется в ускорении газов в одну сторону, а ракеты — в другую.

Но ведь эту задачу можно рассмотреть и с точки зрения сохранения импульса. Если учесть знаки скоростей газа и ракеты, то суммарный импульс окажется равным нулю (он таким и был до сгорания топлива). Импульс сохраняется только потому, что действующие согласно принципу действия-противодействия силы являются внутренними, существующими между частями системы (ракетой и газами).

Как рассматриваемый принцип связан с ускорением всей системы?

Иными словами, как изменятся силы F 12 ¯ и -F 21 ¯, если система, в которой они возникают, будет двигаться ускоренно? Обратимся к примеру с лошадью и телегой. Допустим, вся система начала увеличивать свою скорость, однако силы F 12 ¯ и -F 21 ¯ останутся при этом неизменными. Ускорение возникает за счет увеличения силы, с которой поверхность земли действует на копыта животного, а не за счет уменьшения силы противодействия телеги -F 21 ¯.

Таким образом, взаимодействия внутри системы не зависят от ее внешнего состояния.

Некоторые примеры из жизни

«Приведите примеры третьего закона Ньютона» — это задание часто можно слышать от школьных учителей. Выше уже были приведены примеры с ракетой и лошадью. В списке ниже перечислим еще некоторые:

отталкивание пловца от стенки бассейна: пловец получает ускорение, поскольку на него воздействует стена;
полет птицы: толкая воздух вниз и назад при каждом взмахе крыла, птица получает толчок от воздуха вверх и вперед;
отскок футбольного мяча от стены: проявление противодействия силы реакции стены;
притяжение Земли: с какой силой наша планета притягивает нас вниз, с точно такой же мы воздействуем на нее вверх (для планеты это мизерная сила, она ее «не замечает», а мы — да).

Все эти примеры приводят к важному выводу: любые силовые взаимодействия в природе всегда возникают в виде пары противодействующих сил. Невозможно оказать воздействие на объект, не испытав при этом его противодействие.

Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом

Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!

Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.

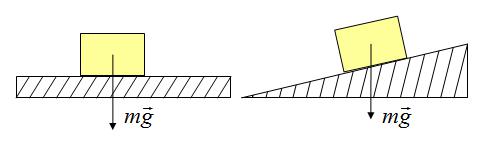
Сила тяжести

На каждое тело, находящееся на планете, действует гравитация Земли . Сила, с которой Земля притягивает каждое тело, определяется по формуле

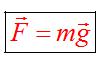
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз .

Сила трения

Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

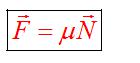
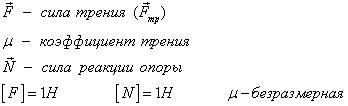
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.

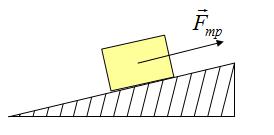
Сила реакции опоры

Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора . Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».

Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.

Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как

Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

Сила упругости

Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.

Закон Гука

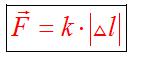
Сила упругости направлена противоположно деформации.

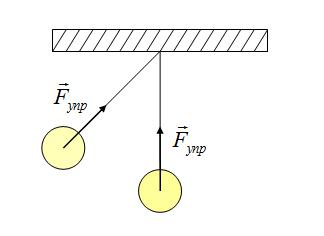
Так как тело представляем в виде материальной точки, силу можно изображать с центра

При последовательном соединении, например, пружин жесткость рассчитывается по формуле

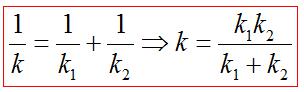
При параллельном соединении жесткость

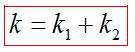
Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.

Подробнее о свойствах твердых тел .

Вес тела

Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!

Формулы определения веса нет. Обозначается эта силы буквой .

Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

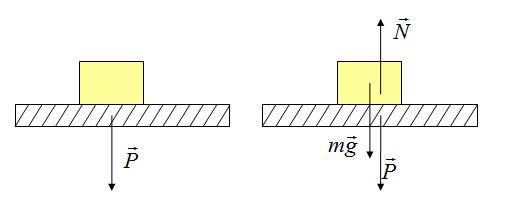
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.

Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью . Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

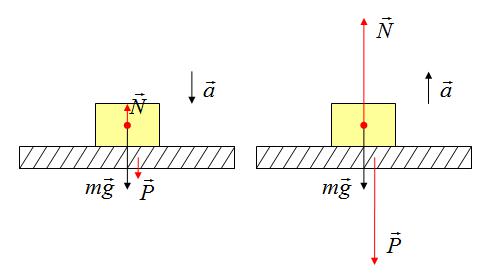
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила

Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!

Перегрузка — отношение веса к силе тяжести

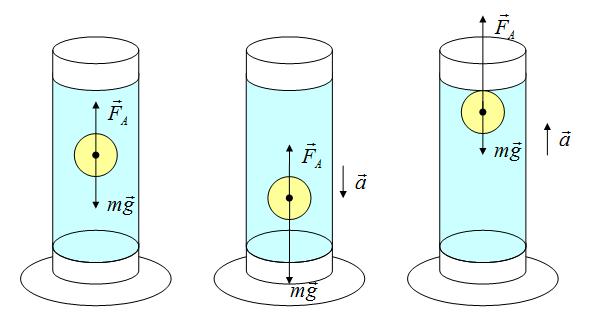
Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

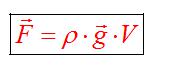
В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.

Электрические силы

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона , сила Ампера , сила Лоренца , подробно рассмотрены в разделе Электричество .

Схематичное обозначение действующих на тело сил

Часто тело моделируют материальной точкой . Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.

Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.

Главное запомнить

1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы

Различают внешнее (сухое) и внутреннее (вязкое) трение. Внешнее трение возникает между соприкасающимися твердыми поверхностями, внутреннее — между слоями жидкости или газа при их относительном движении. Существует три вида внешнего трения: трение покоя, трение скольжения и трение качения. Трение качения определяется по формулеСила сопротивления возникает при движении тела в жидкости или в газе. Величина силы сопротивления зависит от размеров и формы тела, скорости его движения и свойств жидкости или газа. При небольших скоростях движения сила сопротивления пропорциональна скорости тела При больших скоростях пропорциональна квадрату скорости

Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила

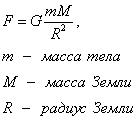
А сейчас сравним закон гравитации и силу тяжести

Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.

Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.

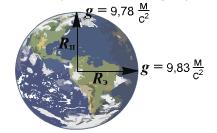
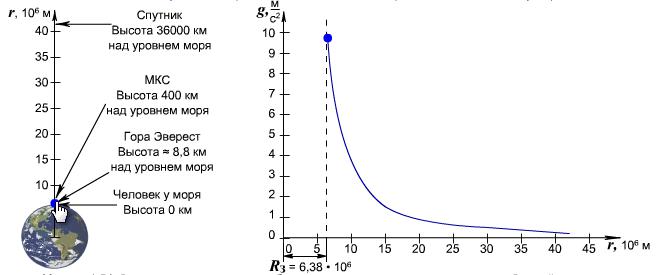
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.

Ускорения тел определяются действующими на них силами. После того как мы научились измерять силу и знаем в принципе, как определять ускорение, можно ответить на главный вопрос: «Как зависит ускорение тела от действующих на него сил?»
Экспериментальное определение зависимости ускорения от силы
Установить на опыте связь между ускорением и силой с абсолютной точностью нельзя, так как любое измерение дает приблизительное значение измеряемой величины. Но подметить характер зависимости ускорения от силы можно с помощью несложных опытов. Уже простые наблюдения показы-вают, что чем больше сила, тем быстрее меняется скорость тела, т. е. тем больше его ускорение. Естественно предположить, что ускорение прямо пропорционально силе. В принципе, конечно, зависимость ускорения от силы может быть более сложной, но сначала надо посмотреть, не справедливо ли самое простое предположение.
Лучше всего изучать поступательное движение тела, например металлического бруска, по горизонтальной поверхности стола, так как только при поступательном движении ускорение всех точек одно и то же, и мы можем говорить об определенном ускорении тела в целом. Однако в этом случае сила трения о стол велика и, главное, ее трудно точно измерить.
Поэтому возьмем тележку с легкими колесами и установим ее на рельсы. Тогда сила трения сравнительно невелика, а мас-
Рис. 2.14
X
Q
о
Рис. 2.13 сой колес можно пренебречь по сравнению с массой тележки, движущейся поступательно (рис. 2.13).
Пусть на тележку действует постоянная сила со стороны ни-ти, к концу которой прикреплен груз. Модуль силы измеряется пружинным динамометром. Эта сила постоянна, но не равна при движении силе, с которой Земля притягивает подвешенный груз. Измерить ускорение тележки непосредственно, определяя изменение ее скорости за малый интервал времени, весьма затруднительно. Но его можно оценить, измеряя время t, затрачиваемое тележкой на прохождение пути s.
Учитывая, что при действии постоянной силы ускорение тоже постоянно, так как оно однозначно определяется силой, можно использовать кинематические формулы равноускоренного движения. При начальной скорости, равной нулю,
at ~2~ где и ¦ Отсюда
начальная и конечная координаты тела. 2s
(2.5.1) Непосредственно на глаз видно, что тележка тем быстрее набирает скорость, чем больше действующая на нее сила. Тщательные измерения модулей силы и ускорения показывают прямую пропорциональность между ними:
а ~ F.
Существуют и другие опыты, подтверждающие эту связь. Вот один из них. Массивный каток (рис. 2.14) установлен на платформе. Если привести платформу во вращение, то каток под действием натянутой нити приобретает центростремительное ускорение, которое легко определить по радиусу вращения R и числу оборотов в секунду п:
а = 4 K2n2R.
Силу найдем из показаний динамометра. Изменяя число оборотов и сопоставляя F и а, убедимся, что F ~ а.
Если на тело одновременно действует несколько сил, то модуль ускорения тела будет пропорционален модулю геометрической суммы всех этих сил, равной:
F = Fj + F2+ … . (2.5.2)
->
Векторы а и F направлены по одной прямой в одну и ту же сторону:
а ~ F. (2.5.3)
Это видно на опыте с тележкой: ускорение тележки направ- ленр вдоль привязанной к ней нити.
Что такое инерция?
Согласно механике Ньютона сила однозначно определяет ускорение тела, но не его скорость. Это нужно очень отчетливо представлять себе. Сила определяет не скорость, а то, как быстро она изменяется. Поэтому покоящееся тело приобретет заметную скорость под действием силы лишь за некоторый интервал времени.
mm

Ускорение возникает сразу, одновременно с началом действия силы, но скорость нарастает постепенно. Даже очень большая сила не в состоянии сообщить телу сразу значительную скорость. Для этого нужно время. Чтобы остановить тело, опять-таки нужно, чтобы тор-мозящая сила, как бы она ни была велика, действовала некоторое время.
Именно эти факты имеют в виду, когда говорят, что тела инертны. Приведем примеры простых опытов, в которых очень наглядно проявляется инертность тел.
1. Массивный шар подвешен на тонкой нити, внизу к нему привязана точно такая же нить (рис. 2.15). Если медленно тянуть за нижнюю Рис. 2.15
нить, то, как и следовало ожидать, рвется верхняя нить. Ведь на нее действует и вес шара, и сила, с которой мы тянем шар вниз. Однако если за нижнюю нить очень быстро дернуть, то оборвется именно она, что на первый взгляд довольно странно. Но это легко объяснить. Когда мы тянем за нить медленно, то шар постепенно опускается, растягивая верхнюю нить до тех пор, пока она не оборвется.
При быстром рывке с большой силой шар получает большое ускорение, но скорость его не успевает увеличиться сколь- ко-нибудь значительно за тот малый промежуток времени, в течение которого нижняя нить сильно растягивается, поэтому именно она и обрывается, а верхняя нить растягивается мало и остается целой.
Интересен опыт с длинной палкой, подвешенной на бумажных кольцах (рис. 2.16). Если резко ударить по палке железным стержнем, то палка ломается, а бумажные кольца остаются невредимыми. Этот опыт вы постарайтесь объяснить сами.
Еще более простой опыт можно выполнить дома. Идея опыта ясна из рисунка 2.17. Левая часть рисунка соответствует ситуации, когда v = const или а = 0. На правой части рисунка v Ф const, т. е. а Ф 0.

Рис. 2.16
Рис. 2.17
Наконец, самый, пожалуй, эффектный опыт. Если выстрелить в пустой пластмассовый сосуд, пуля оставит в стенках отверстия, но сосуд останется целым. Если же выстрелить в такой же сосуд, заполненный водой, то сосуд разорвется на мелкие части. Этот результат опыта объясняется так. Вода очень мало сжимаема, и небольшое изменение ее объема приводит к резкому возрастанию давления. Когда пуля очень быстро входит в воду, пробив стенки сосуда, давление резко возрастает. Из-за инертности воды ее уровень не успевает повыситься и возросшее давление разрывает сосуд на части.
Иногда говорят, что благодаря инерции тело «сопротивляется» попыткам изменить его скорость. Это не совсем верно. Тело всегда меняет скорость под действием силы, но изменение скорости требует времени. Как подчеркивал Дж. Максвелл, говорить о сопротивлении тела попыткам изменить его скорость так же неправильно, как и говорить о том, что чай «сопротивляется» тому, чтобы стать сладким. Просто нужно некоторое время для растворения сахара.
Законы механики и повседневный опыт
Основное утверждение механики достаточно наглядно и не сложно. Оно без особого труда укладывается в нашем сознании. Ведь мы с рождения живем в мире тел, движение которых подчиняется законам механики Ньютона.
Но иногда приобретенные из жизненного опыта представления могут подвести. Так, слишком укоренилось представление о том, что скорость тела направлена в ту же сторону, куда направлена приложенная к нему сила. На самом же деле сила определяет не скорость, а ускорение тела, и направление скорости и силы могут не совпадать. Это хорошо видно на рисунке 2.18.
При движении тела, брошенного под углом к горизонту, сила тяжести все время направлена вниз, и скорость, касательная к траектории, образует с силой некоторый угол, который в процессе полета тела изменяется.
Направление силы совпадает с направлением скорости только в частном случае прямолинейного движения с растущей по модулю скоростью.
Установлен главный для динамики факт: ускорение тела прямо пропорционально действующей на него силе.

1. Нить, на которой подвешен шарик, отклонили на некоторый угол и отпустили. Куда направлена равнодействующая сил, действующих на шарик, в момент, когда нить вертикальна?
2. Начертите на полу небольшой круг и устройте соревнование. Каждый участник быстро идет по прямой в направлении к кругу, держа в руке теннисный мячик. Задача состоит в том, чтобы выпущенный из рук мячик попал в круг. Это соревнование покажет, кто из вас лучше понимает сущность механики Ньютона. Рис. 2.18

Еще по теме § 2.5. СВЯЗЬ МЕЖДУ УСКОРЕНИЕМ И СИЛОЙ:

Авторы Декларации усматривали тесную связь между «естественными и неотъемлемыми правами человека»,
Исследователи справедливо отмечают, что кормильство упрочивало связи между правителями и их вассалами и способствовало
§ 6. Причинная связь между общественно опасным действием (бездействием) и наступившими общественно опасными последствиями

Основной задачей механики является поиск законов механического движения тела под действием приложенных к нему сил. Опытным путем было получено, что при скоростях v≪c , где c — скорость света в вакууме, под действием силы F свободное тело изменяет скорость своего поступательного движения, двигаясь с ускорением a , причем связь силы F и ускорения a линейная:

a = k 1 F ,

где k 1 — положительный коэффициент пропорциональности зависящий от выбора единиц измерения силы и ускорения, постоянный для каждого конкретного тела, но различный для разных тел.

Свойство инерции тела проявляется в том, что под действием силы скорость поступательного движения меняется не мгновенно, а постепенно с соответствующим изменению конечным ускорением a . В качестве меры инертности вводят скалярную величину m , называемую массой тела . Чем выше инертность тела, тем меньшее ускорение приобретается под действием определенной силы. Экспериментально получено, что ускорение зависит от массы обратно пропорционально k 1 =k /m :

где коэффициент пропорциональности k зависит только от выбора системы единиц ускорения, силы и массы и одинаков для различных тел. Если единицы измерения величин относятся к одной системе (например, СИ), то коэффициент k=1 .

Таким образом, ускорение тела прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе тела:

Уравнение () называется основным уравнением динамики . Масса тела m является постоянной величиной, не зависящей ни от состояния движения тела, ни от его положения в пространстве, следовательно для сравнения масс достаточно сравнить ускорения приобретаемые телами под действием одинаковой силы:

m 2 / m 1 = a 1 / a 2 .

Если разделить тело на N частей массой m , то опытным путем установлено, что под действием одинаковой силы целое тело приобретает ускорение в N раз меньше, чем при действии силы на каждую часть по отдельности. Следовательно масса тела является аддитивной величиной — масса тела равна сумме масс ее частей. Масса системы тел равна сумме масс всех тел, входящих в систему. Часто в динамических расчетах тело мысленно разбивают на систему материальных точек имеющих массу. Масса всего тела будет равна сумме масс всех его материальных точек.

Для измерения массы тела можно использовать рычажные весы. Принцип их работы следующий. Поскольку ускорение свободного падения g в одном и том же месте на поверхности Земли одинаковое для всех тел, то на тело будет действовать сила тяжести P удовлетворяющая соотношению

Для двух различных масс

При взвешивании тела на рычажных весах измеряемую массу m 1 уравновешивают с эталонными массами гирь m 2 . В равновесии P 1 =P 2 , а значит и m 1 =m 2 .

В стандартной системе единиц масса измеряется в килограммах (кг).

Уравнение () описывает движение тела только если оно движется поступательно и не деформируется. В противном случае, ускорения различных точек тела будет различным. Материальная точка не может деформироваться или вращаться, поэтому для нее уравнение () всегда будет справедливым.

Если на материальную точку действует несколько сил F i (i =1, …, n ) с результирующей F , то ускорение материальной точки будет:

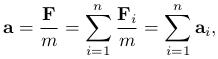
где a i — ускорение материальной точки при действии на нее одной силы F i , то есть действует принцип независимости действия сил — если на материальную точку одновременно действует несколько сил, то каждая из них сообщает материальной точке такое же ускорение, как если бы других сил не было.

Как и любой вектор, можно разложить вектор результирующей силы на две составляющие: касательную к траектории точки F τ и нормальную к ней F n:

F = F τ + F n .

Сравнивая с разложением вектора ускорения на касательную и нормальную составляющую и используя основное уравнение динамики () получим:

Нормальная сила F n меняет только направление вектора v , направлена к центру кривизны траектории радиуса R и называется центростремительной силой :

Касательная сила изменяет величину скорости v : положительная величина F τ ускоряет тело, а отрицательная замедляет; при F τ =0 тело движется равномерно с постоянной скоростью. Если при равномерном движении нормальная сила равна нулю, то траектория будет прямолинейной, если нормальная сила постоянна и отлична от нуля, то траектория будет иметь постоянный радиус кривизны (то есть окружность на плоскости или винтовая линия в пространстве):

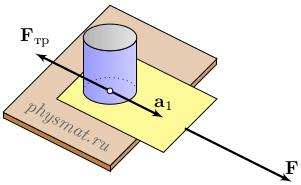
Рис. 1 Опыт по демонстрации инерции

Поместим на горизонтальную поверхность стола лист бумаги, а на нем разместим тело (например, стакан). В начале лист и стакан находятся в состоянии покоя. Если медленно потянуть лист бумаги с силой F , то стакан останется неподвижен относительно листа, но начнет движение с ускорением относительно стола, то есть стакан будет двигаться с таким же ускорением, что и лист бумаги. Если резко потянуть лист бумаги, то он выдернется из под стакана и стакан практически не переместится относительно стола.

Для перемещения стакана на него должна действовать сила, а единственной силой, возникающая в горизонтальном направлении является сила трения F тр возникающая между листом и стаканом. Если ускорение листа бумаги равно a , то в направлении этого ускорения возникает сила F =ma , сила трения направлена в противоположную сторону и равна F тр =-ma для малой силы F , то есть если тянуть лист бумаги медленно, то силы компенсируются и стакан будет неподвижен относительно листа бумаги. С ростом силы F значение силы трения достигает максимального значения F тр =μmg , называемого силой трения скольжения , где μ — коэффициент трения между листом бумаги и стаканом. Если приложить силу F <�μmg , то сила трения уже не сможет ее скомпенсировать полностью и стакан будет двигаться относительно листа под действием силы F —F тр с ускорением a 1 =a -μg , а относительно стола с ускорением a 2 =a —a 1 =μg . Поскольку время, за которое лист бумаги выдергивается из-под стакана мало, то стакан пройдет незначительное расстояние.

Отметим, что после выдергивания листа бумаги стакан имеет ускорение a 2 относительно стола и далее он остановится из-за силы трения между стаканом и столом. Если провести тот же опыт не на столе, а, например, на льду, где коэффициент трения намного меньше (а значит и сила трения скольжения намного меньше), то стакан будет двигаться по инерции под действием меньшей силы и переместится на большее расстояние.

Использованная литература

А.А. Детлаф, Б.М. Яворский, Л.Б. Милковская. Курс физики. М.: Высшая школа. 1973.

Наша кнопка:

Мнение редакции сайта может не совпадать с мнением авторов.
Copyright 2006-2013 сайт. При использовании материалов сайта активная гиперссылка на «сайт» обязательна.
Страница сгенерирована за 0.0039 сек. Хостинг

>>Физика: Связь между ускорением и силой

После того как мы научились измерять силу и знаем, как определять ускорение, можно ответить на главный вопрос: как зависит ускорение тела от действующих на него сил?
Экспериментальное определение зависимости ускорения от силы. Установить на опыте связь между ускорением и силой с абсолютной точностью нельзя, так как любое измерение дает только приблизительное значение измеряемой величины. Но подметить характер зависимости ускорения от силы можно с помощью несложных опытов. Уже простые наблюдения показывают, что, чем больше сила, тем быстрее меняется скорость тела, т. е. больше его ускорение. Естественно предположить, что ускорение прямо пропорционально силе. Ускорение, конечно, может зависеть от силы и гораздо более сложным образом, но сначала надо посмотреть, не справедливо ли самое простое предположение.
Проще всего изучить поступательное движение тела , например металлического бруска, так как только при поступательном движении ускорение всех точек одинаково и мы можем говорить об определенном ускорении тела в целом. Однако в этом случае сила трения о стол довольно велика и, главное, ее трудно точно измерить. Поэтому возьмем установленную на рельсы тележку с легкими колесами. Тогда сила трения будет сравнительно невелика, а массой колес можно пренебречь по сравнению с массой тележки (рис.3.8 ).

Пусть на тележку действует постоянная сила со стороны нити, к концу которой прикреплен груз. Модуль силы измеряется пружинным динамометром. Эта сила постоянна, но не равна при движении силе тяжести, действующей на подвешенный груз. Измерить ускорение тележки непосредственно, определяя изменение ее скорости за малый интервал времени, весьма затруднительно. Но его можно оценить, измеряя время, затрачиваемое тележкой на прохождение пути s .
Предполагая, что при действии постоянной силы ускорение тоже постоянно, так как оно однозначно определяется силой, можно использовать кинематические формулы для равноускоренного движения. При начальной скорости, равной нулю,

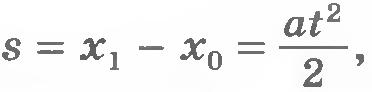
где x 0 и x 1 — начальная и конечная координаты тела. Отсюда

Тщательные измерения модулей сил и ускорений показывают прямую пропорциональность между ними: . Векторы и направлены по одной прямой в одну и ту же сторону.
Если на тело одновременно действуют несколько сил, то ускорение тела будет пропорционально геометрической сумме всех этих сил. Иначе говоря, если:

то
Это положение иногда называют принципом суперпозиции (наложения) сил . Отметим, что действие каждой силы не зависит от наличия других сил.
Что такое инерция ? Итак, согласно механике Ньютона сила однозначно определяет ускорение тела, но не его скорость. Это нужно очень отчетливо представлять себе. Сила определяет не скорость, а то, как быстро она меняется. Поэтому покоящееся тело приобретает заметную скорость под действием силы лишь за некоторый интервал времени.
Ускорение возникает сразу, одновременно с началом действия силы, но скорость нарастает постепенно. Даже очень большая сила не в состоянии сообщить телу сразу значительную скорость. Для этого нужно время. Чтобы остановить тело, опять-таки нужно, чтобы тормозящая сила, как бы она ни была велика, действовала некоторое время.
Именно эти факты имеют в виду, когда говорят, что тела инертны . Приведем примеры простых опытов, в которых очень отчетливо проявляется инертность тел.
1. На рисунке 3.9 изображен массивный шар, подвешенный на тонкой нити. Внизу к шару привязана точно такая же нить. Если медленно тянуть за нижнюю нить, то, как и следует ожидать, порвется верхняя нить: ведь на нее действуют и шар своей тяжестью, и сила, с которой мы тянем шар вниз. Однако если за нижнюю нить очень быстро дернуть, то оборвется именно она, что на первый взгляд довольно странно.

Но это легко объяснить. Когда мы тянем за нить медленно, то шар постепенно опускается, растягивая верхнюю нить до тех пор, пока она не оборвется. При быстром рывке с большой силой разрывается нижняя нить. Шар получает большое ускорение , но скорость его не успевает увеличиться сколько-нибудь значительно за тот малый промежуток времени, в течение которого нижняя нить сильно растягивается и обрывается. Верхняя нить поэтому мало растягивается и остается целой.
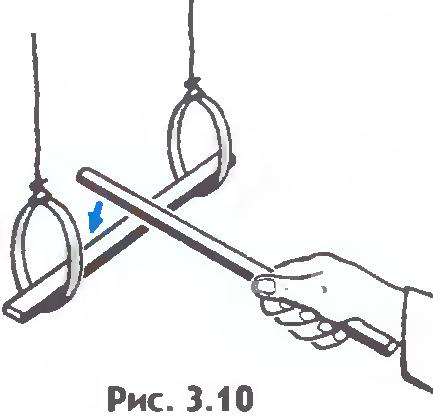
2. Интересен опыт с длинной палкой, подвешенной на бумажных кольцах (рис.3.10 ). Если резко ударить по палке железным стержнем, то палка ломается, а бумажные кольца остаются невредимыми. Этот опыт вы объясните сами.

3. Наконец, самый, пожалуй, эффектный опыт. Если выстрелить в пустой пластмассовый сосуд, пуля оставит в стенках правильные отверстия, но сосуд останется целым. Если же выстрелить в такой же сосуд, заполненный водой, то сосуд разорвется на мелкие части. Это объясняется тем, что вода малосжимаема и небольшое изменение ее объема приводит к резкому возрастанию давления. Когда пуля очень быстро входит в воду, пробив стенку сосуда, давление резко возрастает. Из-за инертности воды ее уровень не успевает повыситься, и возросшее давление разрывает сосуд на части.
Законы механики и повседневный опыт. Основное утверждение механики достаточно наглядно и несложно. Ведь мы с рождения живем в мире тел, движение которых подчиняется законам механики Ньютона.
Но иногда все же приобретенные из жизненного опыта представления могут подвести. Так, слишком сильно укореняется представление о том, что скорость тела будто бы всегда направлена в ту же сторону, куда направлена приложенная к нему сила. На самом же деле это не так. Например, при движении тела, брошенного под произвольным углом к горизонту, сила тяжести направлена вниз, и скорость, касательная к траектории, образует с силой некоторый угол, который в процессе полета тела изменяется.
Сила является причиной возникновения не скорости, а ускорения тела. С направлением силы совпадает во всех случаях направление ускорения, но не скорости.
Установлен главный для динамики факт: ускорение тела прямо пропорционально действующей на него силе.

???
1. Как связано ускорение тела с силой?
2. Что такое инерция! Приведите примеры, демонстрирующие инерцию тел, не указанные в тексте.
3. В каких случаях направление скорости совпадает с направлением силы?

Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку,